MatrixPotential1S¶
About the MatrixPotential1S class¶
The WaveBlocks Project
@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012 R. Bourquin @license: Modified BSD License
Inheritance diagram¶

Class documentation¶
- class WaveBlocks.MatrixPotential1S(expression, variables)¶
This class represents a scalar potential
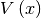 . The potential is given as an
analytical
. The potential is given as an
analytical  matrix expression. Some symbolic calculations with
the potential are supported. For example calculation of eigenvalues and
exponentials and numerical evaluation. Further, there are methods for
splitting the potential into a Taylor expansion and for basis transformations
between canonical and eigenbasis.
matrix expression. Some symbolic calculations with
the potential are supported. For example calculation of eigenvalues and
exponentials and numerical evaluation. Further, there are methods for
splitting the potential into a Taylor expansion and for basis transformations
between canonical and eigenbasis.- calculate_eigenvalues()¶
Calculate the eigenvalue
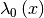 of the potential
of the potential 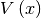 .
In the scalar case this is just the matrix entry
.
In the scalar case this is just the matrix entry 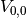 .
.Note
This function is idempotent and the eigenvalues are memoized for later reuse.
- calculate_eigenvectors()¶
Calculate the eigenvector
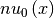 of the potential
of the potential 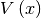 .
In the scalar case this is just the value
.
In the scalar case this is just the value 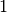 .
.Note
This function is idempotent and the eigenvectors are memoized for later reuse.
- calculate_exponential(factor=1)¶
Calculate the matrix exponential
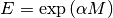 . In this case
the matrix is of size
. In this case
the matrix is of size 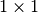 thus the exponential simplifies to the scalar exponential function.
thus the exponential simplifies to the scalar exponential function.Parameters: factor – A prefactor 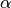 in the exponential.
in the exponential.Note
This function is idempotent.
- calculate_hessian()¶
Calculate the hessian matrix for component
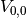 of the potential.
For potentials which depend only one variable
of the potential.
For potentials which depend only one variable 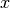 , this equals the second derivative.
, this equals the second derivative.
- calculate_jacobian()¶
Calculate the jacobian matrix for the component
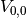 of the potential.
For potentials which depend only one variable
of the potential.
For potentials which depend only one variable 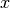 , this equals the first derivative.
, this equals the first derivative.
- calculate_local_quadratic(diagonal_component=None)¶
Calculate the local quadratic approximation
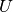 of the potential’s eigenvalue
of the potential’s eigenvalue 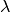 .
.Parameters: diagonal_component – Dummy parameter that has no effect here. Note
This function is idempotent.
- calculate_local_remainder(diagonal_component=None)¶
Calculate the non-quadratic remainder
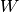 of the quadratic
approximation
of the quadratic
approximation 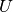 of the potential’s eigenvalue
of the potential’s eigenvalue 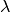 .
This function is used for the homogeneous case and takes into account
the leading component
.
This function is used for the homogeneous case and takes into account
the leading component 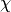 .
.Parameters: diagonal_component – Dummy parameter that has no effect here. Note
This function is idempotent.
- evaluate_at(nodes, component=0, as_matrix=False)¶
Evaluate the potential matrix elementwise at some given grid nodes
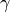 .
.Parameters: - nodes – The grid nodes
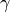 we want to evaluate the potential at.
we want to evaluate the potential at. - component – The component
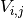 that gets evaluated or ‘None’ to evaluate all.
that gets evaluated or ‘None’ to evaluate all. - as_matrix – Dummy parameter which has no effect here.
Returns: A list with the single entry evaluated at the nodes.
- nodes – The grid nodes
- evaluate_eigenvalues_at(nodes, component=None, as_matrix=False)¶
Evaluate the eigenvalue
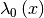 at some grid nodes
at some grid nodes 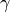 .
.Parameters: - nodes – The grid nodes
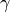 we want to evaluate the eigenvalue at.
we want to evaluate the eigenvalue at. - diagonal_component – Dummy parameter that has no effect here.
- as_matrix – Dummy parameter which has no effect here.
Returns: A list with the single eigenvalue evaluated at the nodes.
- nodes – The grid nodes
- evaluate_eigenvectors_at(nodes)¶
Evaluate the eigenvector
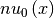 at some grid nodes
at some grid nodes 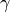 .
.Parameters: nodes – The grid nodes 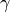 we want to evaluate the eigenvector at.
we want to evaluate the eigenvector at.Returns: A list with the eigenvector evaluated at the given nodes.
- evaluate_exponential_at(nodes)¶
Evaluate the exponential of the potential matrix
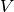 at some grid nodes
at some grid nodes 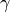 .
.Parameters: nodes – The grid nodes 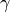 we want to evaluate the exponential at.
we want to evaluate the exponential at.Returns: The numerical approximation of the matrix exponential at the given grid nodes.
- evaluate_hessian_at(nodes, component=None)¶
Evaluate the potential’s hessian at some grid nodes
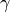 .
.Parameters: - nodes – The grid nodes
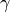 the hessian gets evaluated at.
the hessian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s hessian at the given nodes.
- nodes – The grid nodes
- evaluate_jacobian_at(nodes, component=None)¶
Evaluate the potential’s jacobian at some grid nodes
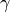 .
.Parameters: - nodes – The grid nodes
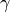 the jacobian gets evaluated at.
the jacobian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s jacobian at the given nodes.
- nodes – The grid nodes
- evaluate_local_quadratic_at(nodes, diagonal_component=None)¶
Numerically evaluate the local quadratic approximation
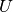 of
the potential’s eigenvalue
of
the potential’s eigenvalue 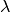 at the given grid nodes
at the given grid nodes 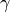 .
This function is used for the homogeneous case.
.
This function is used for the homogeneous case.Parameters: nodes – The grid nodes 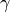 we want to evaluate the quadratic approximation at.
we want to evaluate the quadratic approximation at.Returns: An array containing the values of 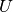 at the nodes
at the nodes 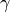 .
.
- evaluate_local_remainder_at(position, nodes, diagonal_component=None, component=None)¶
Numerically evaluate the non-quadratic remainder
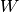 of the quadratic
approximation
of the quadratic
approximation 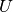 of the potential’s eigenvalue
of the potential’s eigenvalue 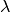 at the given nodes
at the given nodes 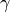 .
This function is used for the homogeneous and the inhomogeneous case and
just evaluates the remainder
.
This function is used for the homogeneous and the inhomogeneous case and
just evaluates the remainder 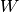 .
.Parameters: - position – The point
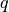 where the Taylor series is computed.
where the Taylor series is computed. - nodes – The grid nodes
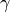 we want to evaluate the potential at.
we want to evaluate the potential at. - component – Dummy parameter that has no effect here.
Returns: A list with a single entry consisting of an array containing the values of
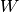 at the nodes
at the nodes 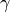 .
.- position – The point
- get_number_components()¶
Returns: The number 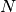 of components the potential supports. In the one dimensional case, it’s just 1.
of components the potential supports. In the one dimensional case, it’s just 1.
- potential = None¶
The matrix of the potential
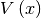 .
.
- project_to_canonical(nodes, values, basis=None)¶
Project a given vector from the potential’s eigenbasis to the canonical basis.
Parameters: - nodes – The grid nodes
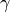 for the pointwise transformation.
for the pointwise transformation. - values – The list of vectors
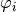 containing the values we want to transform.
containing the values we want to transform. - basis – A list of basis vectors
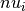 . Allows to use this function for external data, similar to a static function.
. Allows to use this function for external data, similar to a static function.
Returns: This method does nothing and returns the values.
- nodes – The grid nodes
- project_to_eigen(nodes, values, basis=None)¶
Project a given vector from the canonical basis to the eigenbasis of the potential.
Parameters: - nodes – The grid nodes
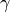 for the pointwise transformation.
for the pointwise transformation. - values – The list of vectors
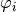 containing the values we want to transform.
containing the values we want to transform. - basis – A list of basisvectors
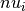 . Allows to use this function for external data, similar to a static function.
. Allows to use this function for external data, similar to a static function.
Returns: This method does nothing and returns the values.
- nodes – The grid nodes
- x = None¶
The variable
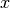 that represents position space.
that represents position space.