MatrixPotentialMS¶
About the MatrixPotentialMS class¶
The WaveBlocks Project
@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012 R. Bourquin @license: Modified BSD License
Inheritance diagram¶

Class documentation¶
- class WaveBlocks.MatrixPotentialMS(expression, variables)¶
This class represents a matrix potential
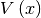 . The potential is given as an analytical
expression with a matrix of size bigger than
. The potential is given as an analytical
expression with a matrix of size bigger than 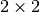 . Some calculations
with the potential are supported. For example calculation of eigenvalues and
exponentials and numerical evaluation. Further, there are methods for
splitting the potential into a Taylor expansion and for basis transformations
between canonical and eigenbasis. All methods use numerical techniques because
symbolical calculations are unfeasible.
. Some calculations
with the potential are supported. For example calculation of eigenvalues and
exponentials and numerical evaluation. Further, there are methods for
splitting the potential into a Taylor expansion and for basis transformations
between canonical and eigenbasis. All methods use numerical techniques because
symbolical calculations are unfeasible.- calculate_eigenvalues()¶
Calculate the eigenvalues
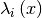 of the potential
of the potential 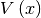 .
We do the calculations with numerical tools. The multiplicities are taken into account.
.
We do the calculations with numerical tools. The multiplicities are taken into account.Note
Note: the eigenvalues are memoized for later reuse.
- calculate_eigenvectors()¶
Calculate the two eigenvectors
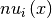 of the potential
of the potential 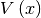 .
We do the calculations with numerical tools.
.
We do the calculations with numerical tools.Note
The eigenvectors are memoized for later reuse.
- calculate_exponential(factor=1)¶
Calculate the matrix exponential
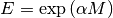 . In the case where
the matrix is of size bigger than
. In the case where
the matrix is of size bigger than 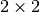 symbolical calculations become
unfeasible. We use numerical approximations to determine the matrix exponential.
symbolical calculations become
unfeasible. We use numerical approximations to determine the matrix exponential.Parameters: factor – A prefactor 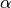 in the exponential.
in the exponential.
- calculate_hessian()¶
Calculate the hessian matrix for each component
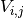 of the potential.
For potentials which depend only one variable
of the potential.
For potentials which depend only one variable 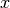 , this equals the second derivative.
, this equals the second derivative.
- calculate_jacobian()¶
Calculate the jacobian matrix for each component
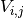 of the potential.
For potentials which depend only one variable
of the potential.
For potentials which depend only one variable 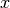 , this equals the first derivative.
, this equals the first derivative.
- calculate_local_quadratic(diagonal_component=None)¶
Calculate the local quadratic approximation matrix
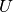 of the potential’s
eigenvalues in
of the potential’s
eigenvalues in 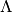 . This function can be used for the homogeneous case
and takes into account the leading component
. This function can be used for the homogeneous case
and takes into account the leading component 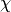 .
If the parameter
.
If the parameter 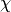 is not given, calculate the local quadratic approximation
matrix
is not given, calculate the local quadratic approximation
matrix 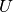 of all the potential’s eigenvalues in
of all the potential’s eigenvalues in 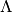 . This function is used
for the inhomogeneous case.
. This function is used
for the inhomogeneous case.Parameters: diagonal_component – Specifies the index 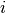 of the eigenvalue
of the eigenvalue 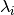 that gets expanded into a Taylor series
that gets expanded into a Taylor series 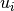 .
.
- calculate_local_remainder(diagonal_component=None)¶
Calculate the non-quadratic remainder matrix
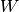 of the quadratic
approximation matrix
of the quadratic
approximation matrix 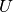 of the potential’s eigenvalue matrix
of the potential’s eigenvalue matrix 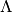 .
This function is used for the homogeneous case and takes into account the leading component
.
This function is used for the homogeneous case and takes into account the leading component 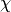 .
.Parameters: diagonal_component – Specifies the index 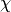 of the leading component
of the leading component 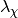 .
.
- evaluate_at(nodes, component=None, as_matrix=True)¶
Evaluate the potential matrix elementwise at some given grid nodes
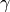 .
.Parameters: - nodes – The grid nodes
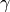 we want to evaluate the potential at.
we want to evaluate the potential at. - component – The component
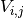 that gets evaluated or ‘None’ to evaluate all.
that gets evaluated or ‘None’ to evaluate all. - as_matrix – Returns the whole matrix
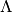 instead of only a list with the eigenvalues
instead of only a list with the eigenvalues 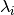 .
.
Returns: A list with the
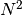 entries evaluated at the nodes.
entries evaluated at the nodes.- nodes – The grid nodes
- evaluate_eigenvalues_at(nodes, component=None, as_matrix=False)¶
Evaluate the eigenvalues
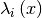 at some grid nodes
at some grid nodes 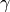 .
.Parameters: - nodes – The grid nodes
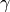 we want to evaluate the eigenvalues at.
we want to evaluate the eigenvalues at. - component – The index
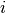 of the eigenvalue
of the eigenvalue 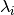 that gets evaluated.
that gets evaluated. - as_matrix – Returns the whole matrix
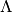 instead of only a list with the eigenvalues
instead of only a list with the eigenvalues 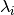 .
.
Returns: A sorted list with
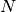 entries for all the eigenvalues evaluated at the nodes. Or a single value if a component was specified.
entries for all the eigenvalues evaluated at the nodes. Or a single value if a component was specified.- nodes – The grid nodes
- evaluate_eigenvectors_at(nodes)¶
Evaluate the eigenvectors
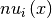 at some grid nodes
at some grid nodes 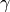 .
.Parameters: nodes – The grid nodes 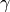 we want to evaluate the eigenvectors at.
we want to evaluate the eigenvectors at.Returns: A list with the 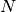 eigenvectors evaluated at the given nodes.
eigenvectors evaluated at the given nodes.
- evaluate_exponential_at(nodes)¶
Evaluate the exponential of the potential matrix
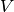 at some grid nodes
at some grid nodes 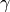 .
For matrices of size
.
For matrices of size 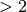 we do completely numerical exponentation.
we do completely numerical exponentation.Parameters: nodes – The grid nodes 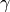 we want to evaluate the exponential at.
we want to evaluate the exponential at.Returns: The numerical approximation of the matrix exponential at the given grid nodes.
- evaluate_hessian_at(nodes, component=None)¶
Evaluate the hessian at some grid nodes
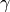 for each component
for each component 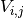 of the potential.
of the potential.Parameters: - nodes – The grid nodes
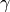 the hessian gets evaluated at.
the hessian gets evaluated at. - component – The index tuple
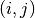 that specifies the potential’s entry of which the hessian is evaluated. (Or ‘None’ to evaluate all)
that specifies the potential’s entry of which the hessian is evaluated. (Or ‘None’ to evaluate all)
Returns: Either a list or a single value depending on the optional parameters.
- nodes – The grid nodes
- evaluate_jacobian_at(nodes, component=None)¶
Evaluate the jacobian at some grid nodes
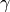 for each component
for each component 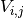 of the potential.
of the potential.Parameters: - nodes – The grid nodes
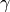 the jacobian gets evaluated at.
the jacobian gets evaluated at. - component – The index tuple
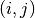 that specifies the potential’s entry of which the jacobian is evaluated. (Defaults to ‘None’ to evaluate all)
that specifies the potential’s entry of which the jacobian is evaluated. (Defaults to ‘None’ to evaluate all)
Returns: Either a list or a single value depending on the optional parameters.
- nodes – The grid nodes
- evaluate_local_quadratic_at(nodes, diagonal_component)¶
Numerically evaluate the local quadratic approximation matrix
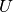 of
the potential’s eigenvalues in
of
the potential’s eigenvalues in 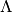 at the given grid nodes
at the given grid nodes 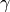 .
.Parameters: - nodes – The grid nodes
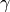 we want to evaluate the quadratic approximation at.
we want to evaluate the quadratic approximation at. - diagonal_component – Specifies the index
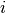 of the eigenvalue
of the eigenvalue 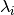 that gets expanded into a Taylor series
that gets expanded into a Taylor series 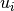 .
.
Returns: A list of arrays or a single array containing the values of
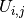 at the nodes
at the nodes 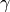 .
.- nodes – The grid nodes
- evaluate_local_remainder_at(position, nodes, diagonal_component=None, component=None)¶
Numerically evaluate the non-quadratic remainder matrix
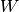 of the quadratic
approximation matrix
of the quadratic
approximation matrix 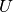 of the potential’s eigenvalues in
of the potential’s eigenvalues in 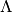 at the
given nodes
at the
given nodes 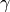 . This function is used for the homogeneous and the
inhomogeneous case and just evaluates the remainder matrix
. This function is used for the homogeneous and the
inhomogeneous case and just evaluates the remainder matrix 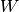 .
.Parameters: - position – The point
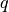 where the Taylor series is computed.
where the Taylor series is computed. - nodes – The grid nodes
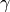 we want to evaluate the potential at.
we want to evaluate the potential at. - component – The component
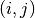 of the remainder matrix
of the remainder matrix 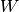 that is evaluated.
that is evaluated.
Returns: A list with a single entry consisting of an array containing the values of
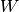 at the nodes
at the nodes 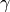 .
.- position – The point
- get_number_components()¶
Returns: The number 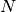 of components the potential supports. This is also the size of the matrix.
of components the potential supports. This is also the size of the matrix.
- potential = None¶
The matrix of the potential
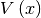 .
.
- project_to_canonical(nodes, values, basis=None)¶
Project a given vector from the potential’s eigenbasis to the canonical basis.
Parameters: - nodes – The grid nodes
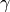 for the pointwise transformation.
for the pointwise transformation. - values – The list of vectors
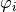 containing the values we want to transform.
containing the values we want to transform. - basis – A list of basis vectors
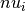 . Allows to use this function for external data, similar to a static function.
. Allows to use this function for external data, similar to a static function.
Returns: Returned is another list containing the projection of the values into the eigenbasis.
- nodes – The grid nodes
- project_to_eigen(nodes, values, basis=None)¶
Project a given vector from the canonical basis to the eigenbasis of the potential.
Parameters: - nodes – The grid nodes
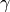 for the pointwise transformation.
for the pointwise transformation. - values – The list of vectors
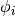 containing the values we want to transform.
containing the values we want to transform. - basis – A list of basisvectors
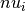 . Allows to use this function for external data, similar to a static function.
. Allows to use this function for external data, similar to a static function.
Returns: Returned is another list containing the projection of the values into the eigenbasis.
- nodes – The grid nodes
- x = None¶
The variable
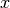 that represents position space.
that represents position space.