DirectHomogeneousQuadrature¶

About the `DirectHomogeneousQuadrature` class¶

The WaveBlocks Project

Inheritance diagram¶

Class documentation¶

class WaveBlocksND.DirectHomogeneousQuadrature(QR=None)[source]¶

do_quadrature(row, col)[source]¶

Evaluates by standard quadrature the integral $\langle \Phi_i | f | \Phi_j \rangle$ for a polynomial function $f(x)$ with $x \in \mathbb{R}^D$ .

Parameters:	row – The index $i$ of the component $\Phi_i$ of $\Psi$ . row – The index $j$ of the component $\Phi_j$ of $\Psi$ .
Returns:	A complex valued matrix of shape $\|\mathfrak{K}_i\| \times \|\mathfrak{K}_j\|$ .

get_description()[source]¶: Return a description of this quadrature object. A description is a dict containing all key-value pairs necessary to reconstruct the current instance. A description never contains any data.

get_qr()¶

Return the QuadratureRule subclass instance used for quadrature.

Returns:	The current instance of the quadrature rule.

initialize_operator(operator=None, matrix=False, eval_at_once=False)[source]¶

Provide the operator part of the inner product to evaluate. This function initializes the operator used for quadratures and for building matrices.

Parameters:	operator – The operator of the inner product. If `None` a suitable identity is used. matrix – Set this to `True` (Default is `False`) in case we want to compute the matrix elements. For nasty technical reasons we can not yet unify the operator call syntax. eval_at_once (Boolean, default is `False`.) – Flag to tell whether the operator supports the `entry=(r,c)` call syntax.

initialize_packet(packet)[source]¶

Provide the wavepacket part of the inner product to evaluate. Since the quadrature is homogeneous the same wavepacket is used for the ‘bra’ as well as the ‘ket’ part.

Parameters:	packet – The packet that is used for the ‘bra’ and ‘ket’ part.

perform_build_matrix(row, col)¶

Computes by standard quadrature the matrix elements $\langle\Phi_i | f |\Phi^\prime_j\rangle$ for a general function $f(x)$ with $x \in \mathbb{R}^D$ .

Parameters:	row – The index $i$ of the component $\Phi_i$ of $\Psi$ . row – The index $j$ of the component $\Phi^\prime_j$ of $\Psi^\prime$ .
Returns:	A complex valued matrix of shape $\|\mathfrak{K}_i\| \times \|\mathfrak{K}^\prime_j\|$ .

perform_quadrature(row, col)¶

Evaluates by numerical steepest descent the integral $\langle \Phi_i | f | \Phi^\prime_j \rangle$ for a polynomial function $f(x)$ with $x \in \mathbb{R}^D$ .

Parameters:	row – The index $i$ of the component $\Phi_i$ of $\Psi$ . row – The index $j$ of the component $\Phi^\prime_j$ of $\Psi^\prime$ .
Returns:	A single complex floating point number.

prepare(rows, cols)[source]¶

Precompute some values needed for evaluating the quadrature $\langle \Phi_i | f(x) | \Phi_j \rangle$ or the corresponding matrix over the basis functions of $\Phi_i$ and $\Phi_j$ .

Parameters:	rows – A list of all $i$ with $0 \leq i \leq N$ selecting the $\Phi_i$ for which we precompute values. cols – A list of all $j$ with $0 \leq j \leq N$ selecting the $\Phi_j$ for which we precompute values.

set_qr(QR)¶

Set the QuadratureRule subclass instance used for quadrature.

Parameters:	QR – The new `QuadratureRule` instance.

transform_nodes(Pi, eps, *, QR=None)[source]¶

Transform the quadrature nodes $\gamma$ such that they fit the given wavepacket $\Phi\left[\Pi\right]$ .

Parameters:	Pi – The parameter set 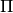$\Pi$ of the wavepacket. eps – The value of $\varepsilon$ of the wavepacket. QR – An optional quadrature rule $\Gamma = (\gamma, \omega)$ providing the nodes. If not given the internal quadrature rule will be used.
Returns:	A two-dimensional ndarray of shape $(D, \|\Gamma\|)$ where $\|\Gamma\|$ denotes the total number of quadrature nodes.