GaussLaguerreQR

About the GaussLaguerreQR class

The WaveBlocks Project

@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License

Inheritance diagram

Inheritance diagram of GaussLaguerreQR

Class documentation

class WaveBlocksND.GaussLaguerreQR(order, a=-0.5, options={})[source]

This class implements a (generalized) Gauss-Laguerre quadrature rule.

__init__(order, a=-0.5, options={})[source]

Initialize a new quadrature rule.

Parameters:
  • order – The order k of the Gauss-Laguerre quadrature. From theory we know that a Gauss quadrature rule of order k is exact for polynomials up to degree 2 k - 1.
  • a – The parameter a > -1 of the generalized Gauss-Laguerre quadrature. This value defaults to 0 resulting in classical Gauss-Laguerre quadrature.
Raise:

ValueError if order order is not 1 or above.

Warning

This quadrature is made specifically for our needs. Therefore the default values of \alpha is not 0 but set to -\frac{1}{2}. There is hope that this will give less confusion and hidden errors.

get_description()[source]

Return a description of this quadrature rule object. A description is a dict containing all key-value pairs necessary to reconstruct the current instance. A description never contains any data.

get_dimension()
Returns:The space dimension 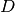D of the quadrature rule.
get_nodes()[source]

Returns the quadrature nodes \{\gamma_i\}_i.

Returns:An array containing the quadrature nodes \{\gamma_i\}_i.
get_number_nodes()
Returns:The number of quadrature nodes denoted by |\Gamma| that are part of this quadrature rule \Gamma = (\gamma, \omega).
get_weights()[source]

Returns the quadrature weights \{\omega_i\}_i.

Returns:An array containing the quadrature weights \{\omega_i\}_i.