GaussianIntegral

About the GaussianIntegral class

The WaveBlocks Project

@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License

Inheritance diagram

Inheritance diagram of GaussianIntegral

Class documentation

class WaveBlocksND.GaussianIntegral(*unused, **kunused)[source]
exact_result_gauss(Pibra, Piket, D, eps)[source]

Compute the overlap integral \langle \phi_{\underline{0}} | \phi_{\underline{0}} \rangle of the groundstate \phi_{\underline{0}} by using the symbolic formula:

\langle \phi_{\underline{0}} | \phi_{\underline{0}} \rangle & = \int C \exp\left(-\frac{1}{2} \underline{x}^{\mathrm{T}} \mathbf{A} \underline{x} +\underline{b}^{\mathrm{T}} \underline{x} + c \right) \mathrm{d}\underline{x} \\ & = C \sqrt{\frac{\left(2\pi\right)^D}{\det \mathbf{A}}} \exp\left(-\frac{1}{2} \underline{b}^{\mathrm{T}} \mathbf{A}^{-\mathrm{H}} \underline{b}\right) \exp\left(c\right)

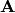In a first step we combine the exponential parts of both wavepackets into \underline{x}^{\mathrm{H}} \mathbf{A} \underline{x} + \underline{b}^{\mathrm{T}} \underline{x} + c. Then we transform \mathbf{A}, \underline{b} and c such that this matches the integrand above. The necessary transformations read:

\mathbf{A}^{\prime} &= -2 \frac{i}{\varepsilon^2} \mathbf{A} \\ \underline{b}^{\prime} &= \frac{i}{\varepsilon^2} \underline{b} \\ c &= \frac{i}{\varepsilon^2} c

Note that this is an internal method and usually there is no reason to call it from outside.

Parameters:
  • Pibra – The parameter set \Pi = \{q_1,p_1,Q_1,P_1\} of the bra \langle \phi_0 |.
  • Piket – The parameter set \Pi^\prime = \{q_2,p_2,Q_2,P_2\} of the ket | \phi_0 \rangle.
  • D – The space dimension 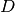D the packets have.
  • eps – The semi-classical scaling parameter \varepsilon.
Returns:

The value of the integral \langle \phi_{\underline{0}} | \phi_{\underline{0}} \rangle.
get_description()[source]

Return a description of this integral object. A description is a dict containing all key-value pairs necessary to reconstruct the current instance. A description never contains any data.

get_qr()

Return the QuadratureRule subclass instance used for quadrature.

Returns:The current instance of the quadrature rule.
initialize_operator(operator=None, matrix=False, eval_at_once=False)[source]

Provide the operator part of the inner product to evaluate. This function initializes the operator used for quadratures and for building matrices.

Note

The symbolic Gaussian integral formula can not handle operators at all.

Parameters:
  • operator – The operator of the inner product. If None a suitable identity is used.
  • matrix – Set this to True (Default is False) in case we want to compute the matrix elements. For nasty technical reasons we can not yet unify the operator call syntax.
  • eval_at_once (Boolean, default is False.) – Flag to tell whether the operator supports the entry=(r,c) call syntax. Since we do not support operators at all, it has no effect.
initialize_packet(pacbra, packet=None)[source]

Provide the wavepacket parts of the inner product to evaluate. Since the formula is for the inhomogeneous case explicitly, different wavepackets can be used for the ‘bra’ as well as the ‘ket’ part.

Parameters:
  • pacbra – The packet that is used for the ‘bra’ part.
  • packet – The packet that is used for the ‘ket’ part.
perform_build_matrix(row, col)[source]

Computes the matrix elements \langle\Phi_i |\Phi^\prime_j\rangle by an exact symbolic formula.

Warning

This method does only take into account the ground state basis components \phi_{\underline{0}} from both, the ‘bra’ and the ‘ket’. If the wavepacket \Phi contains higher order basis functions \phi_{\underline{k}} with non-zero coefficients c_{\underline{k}}, the inner products computed are wrong! There is also no warning about that.

Parameters:
  • row – The index i of the component \Phi_i of \Psi.
  • row – The index j of the component \Phi^\prime_j of \Psi^\prime.
Returns:

A complex valued matrix of shape |\mathfrak{K}_i| \times |\mathfrak{K}^\prime_j|.
perform_quadrature(row, col)[source]

Evaluates the integral \langle \Phi_i | \Phi^\prime_j \rangle by an exact symbolic formula.

Warning

This method does only take into account the ground state basis components \phi_{\underline{0}} from both, the ‘bra’ and the ‘ket’. If the wavepacket \Phi contains higher order basis functions \phi_{\underline{k}} with non-zero coefficients c_{\underline{k}}, the inner products computed are wrong! There is also no warning about that.

Parameters:
  • row – The index i of the component \Phi_i of \Psi.
  • row – The index j of the component \Phi^\prime_j of \Psi^\prime.
Returns:

A single complex floating point number.
prepare(rows, cols)[source]

Precompute some values needed for evaluating the integral \langle \Phi_i | \Phi^\prime_j \rangle or the corresponding matrix over the basis functions of \Phi_i and \Phi^\prime_j. Note that this function does nothing in the current implementation.

Parameters:
  • rows – A list of all i with 0 \leq i \leq N selecting the \Phi_i for which we precompute values.
  • cols – A list of all j with 0 \leq j \leq N selecting the \Phi^\prime_j for which we precompute values.
set_qr(QR)

Set the QuadratureRule subclass instance used for quadrature.

Parameters:QR – The new QuadratureRule instance.