HagedornWavepacketInhomogeneous¶

About the `HagedornWavepacketInhomogeneous` class¶

The WaveBlocks Project

Inheritance diagram¶

Class documentation¶

class WaveBlocksND.HagedornWavepacketInhomogeneous(dimension, ncomponents, eps)[source]¶

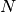This class represents inhomogeneous vector valued Hagedorn wavepackets $\Psi$ with $N$ components in 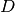$D$ space dimensions.

__init__(dimension, ncomponents, eps)[source]¶

Initialize a new in homogeneous Hagedorn wavepacket.

Parameters:	dimension – The space dimension 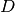$D$ the packet has. ncomponents – The number 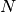$N$ of components the packet has. eps – The semi-classical scaling parameter $\varepsilon$ of the basis functions.
Returns:	An instance of `HagedornWavepacketInhomogeneous`.

__str__()[source]¶

Returns:	A string describing the Hagedorn wavepacket $\Psi$ .

evaluate_at(grid, *, component=None, prefactor=False)¶

Evaluate the Hagedorn wavepacket $\Psi$ at the given nodes $\gamma$ .

Parameters:	grid (A class having a `get_nodes(...)()` method.) – The grid $\Gamma$ containing the nodes $\gamma$ . component – The index $i$ of a single component $\Phi_i$ to evaluate. (Defaults to `None` for evaluating all components.) prefactor (Boolean, default is `False`.) – Whether to include a factor of $\frac{1}{\sqrt{\det(Q)}}$ .
Returns:	A list of arrays or a single array containing the values of the $\Phi_i$ at the nodes $\gamma$ .

evaluate_basis_at(grid, component, *, prefactor=False)¶

Evaluate the basis functions $\phi_k$ recursively at the given nodes $\gamma$ .

Parameters:	grid (A class having a `get_nodes(...)()` method.) – The grid $\Gamma$ containing the nodes $\gamma$ . component – The index $i$ of a single component $\Phi_i$ to evaluate. prefactor (Boolean, default is `False`.) – Whether to include a factor of $\frac{1}{\sqrt{\det(Q)}}$ .
Returns:	A two-dimensional ndarray $H$ of shape $(\|\mathfrak{K}_i\|, \|\Gamma\|)$ where the entry $H[\mu(k), i]$ is the value of $\phi_k(\gamma_i)$ .

gen_id()¶: Generate an (unique) ID per wavepacket instance.

Note

The packet id is a string of length 32 because this is exactly the length of an ‘md5’ digest in hex representation.

get_basis_shapes(*, component=None)¶

Retrieve the basis shapes $\mathfrak{K}_i$ for each component $i$ .

Parameters:	component (int) – The component $i$ whose basis shape we request. (Default is `None` which means to return the basis shapes for all components.
Returns:	The basis shape for an individual component or a list with all shapes.

get_coefficient(component, index)¶

Retrieve a single coefficient $c^i_k$ of the specified component $\Phi_i$ of $\Psi$ .

Parameters:	component – The index $i$ of the component $\Phi_i$ we want to update. index (A tuple of 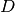$D$ integers.) – The multi-index $k$ of the coefficient $c^i_k$ we want to update.
Returns:	A single complex number.
Raise:	`ValueError` For invalid indices $i$ or $k$ .

get_coefficient_vector(*, component=None)¶

Retrieve the coefficients for all components $\Phi_i$ simultaneously.

Warning

This function does not copy the input data! This is for efficiency as this routine is used in the innermost loops.

Parameters:	component (int) – The component $i$ whose coefficients we request. (Default is `None` which means to return the coefficients for all components.
Returns:	The coefficients $c^i$ of all components $\Phi_i$ stacked into a single long column vector.

get_coefficients(*, component=None)¶

Returns the coefficients $c^i$ for some component $\Phi_i$ of $\Psi$ or all the coefficients $c$ of all components.

Note: this method copies the data arrays.

Parameters:	component (int (Default is `None` meaning all)) – The index $i$ of the component we want to retrieve.
Returns:	A single ndarray with the coefficients of the given component or a list containing the ndarrays for each component. Each ndarray is two-dimensional with a shape of $(\|\mathfrak{K}_i\|, 1)$ .
Raise:	`ValueError` For invalid component indices $i$ .

get_description()[source]¶: Return a description of this wavepacket object. A description is a dict containing all key-value pairs necessary to reconstruct the current instance. A description never contains any data.

get_dimension()¶

Returns:	The space dimension 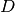$D$ of the wavepacket $\Psi$ .

get_eps()¶

Retrieve the semi-classical scaling parameter $\varepsilon$ of the wavepacket.

Returns:	The value of $\varepsilon$ .

get_gradient_operator()¶

Return the Gradient subclass suitable for computing gradients of this wavepacket.

Returns:	A `GradientHAWP` instance.

get_id()¶

Return the packet ID of this wavepacket instance. The ID may be used for storing packets in associative lists.

Returns:	The ID of the current instance.

get_innerproduct()¶

Return the InnerProduct subclass instance used computing inner products and evaluating brakets.

Returns:	The current `InnerProduct` subclass instance.

get_number_components()¶

Returns:	The number 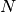$N$ of components the wavepacket $\Psi$ has.

get_parameters(component=None, aslist=False, key=('q', 'p', 'Q', 'P', 'S'))[source]¶

Get the Hagedorn parameter set $\Pi_i$ of each component :math`Phi_i` of the wavepacket $\Psi$ .

Parameters:	component – The index $i$ of the component $\Phi_i$ whose parameters $\Pi_i$ we want to get. aslist – Dummy parameter for API compatibility with the homogeneous packets.
Returns:	A list with all parameter sets $\Pi_i$ or a single parameter set. The parameters $\Pi_i = (q_i, p_i, Q_i, P_i, S_i)$ are always in this order.

norm(component=None, summed=False)¶

Calculate the 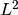$L^2$ norm $\langle\Psi|\Psi\rangle$ of the wavepacket $\Psi$ .

Parameters:	component (int or `None`.) – The index $i$ of the component $\Phi_i$ whose norm is calculated. The default value is `None` which means to compute the norms of all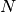 $N$ components. summed (Boolean, default is `False`.) – Whether to sum up the norms $\langle\Phi_i\|\Phi_i\rangle$ of the individual components $\Phi_i$ .
Returns:	The norm of $\Psi$ or the norm of $\Phi_i$ or a list with the 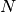$N$ norms of all components. Depending on the values of `component` and `summed`.

set_basis_shapes(basis_shape, *, component=None)¶

Set the basis shape $\mathfrak{K}$ of a given component or for all components.

Parameters:	basis_shape (A subclass of `BasisShape`.) – The basis shape for an individual component or a list with all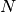 $N$ shapes. component (int) – The component $i$ whose basis shape we want to set. (Default is `None` which means to set the basis shapes for all components.

set_coefficient(component, index, value)¶

Set a single coefficient $c^i_k$ of the specified component $\Phi_i$ of $\Psi$ .

Parameters:	component – The index $i$ of the component $\Phi_i$ we want to update. index (A tuple of 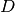$D$ integers.) – The multi-index $k$ of the coefficient $c^i_k$ we want to update. value – The new value of the coefficient $c^i_k$ .
Raise:	`ValueError` For invalid indices $i$ or $k$ .

set_coefficient_vector(vector)¶

Set the coefficients for all components $\Phi_i$ simultaneously.

Warning

This function does not copy the input data! This is for efficiency as this routine is used in the innermost loops.

Parameters:	vector (A two-dimensional ndarray of appropriate shape.) – The coefficients of all components as a single long column vector.

set_coefficients(values, *, component=None)¶

Update all the coefficients $c$ of $\Psi$ or update the coefficients $c^i$ of the components $\Phi_i$ only.

Note: this method copies the data arrays.

Parameters:	values (An ndarray of suitable shape or a list of ndarrays.) – The new values of the coefficients $c^i$ of $\Phi_i$ . component (int (Default is `None` meaning all)) – The index $i$ of the component we want to update with new coefficients.
Raise:	`ValueError` For invalid component indices $i$ .

set_id(anid)¶

Manually set a new ID for the current wavepacket instance.

Parameters:	anid (str) – The new ID.

set_innerproduct(innerproduct)¶

Set the InnerProduct subclass instance used for computing inner products and evaluating brakets.

Parameters:	innerproduct – The new `InnerProduct` subclass instance.

set_parameters(Pi, component=None, key=('q', 'p', 'Q', 'P', 'S'))[source]¶

Set the Hagedorn parameter set $\Pi_i$ of each component :math`Phi_i` of the wavepacket $\Psi$ .

Parameters:	Pi (A single tuple or a list of tuples) – The parameter sets $\Pi_i = (q_i, p_i, Q_i, P_i, S_i)$ with its values in this order. component – The index $i$ of the component $\Phi_i$ whose parameters $\Pi_i$ we want to update.

slim_recursion(grid, component, *, prefactor=False)¶

Evaluate the Hagedorn wavepacket $\Psi$ at the given nodes $\gamma$ . This routine is a slim version compared to the full basis evaluation. At every moment we store only the data we really need to compute the next step until we hit the highest order basis functions.

Parameters:	grid (A class having a `get_nodes(...)()` method.) – The grid $\Gamma$ containing the nodes $\gamma$ . component – The index $i$ of a single component $\Phi_i$ to evaluate. prefactor (Boolean, default is `False`.) – Whether to include a factor of $\frac{1}{\sqrt{\det(Q)}}$ .
Returns:	A list of arrays or a single array containing the values of the $\Phi_i$ at the nodes $\gamma$ .

Note that this function does not include the global phase $\exp(\frac{i S}{\varepsilon^2})$ .

HagedornWavepacketInhomogeneous¶

About the `HagedornWavepacketInhomogeneous` class¶

Inheritance diagram¶

Class documentation¶

Table Of Contents

Previous topic

Next topic

This Page

HagedornWavepacketInhomogeneous¶

About the HagedornWavepacketInhomogeneous class¶

Inheritance diagram¶

Class documentation¶

About the `HagedornWavepacketInhomogeneous` class¶