HagedornWavepacketTransformPhiPsi¶

About the `HagedornWavepacketTransformPhiPsi` class¶

The WaveBlocks Project

class WaveBlocksND.HagedornWavepacketTransformPhiPsi[source]¶

Implementation of the unitary transformation between old-kind Hagedorn wavepackets $\Phi[\Pi]$ and new-kind Hagedorn wavepackets $\Psi[\Pi]$ .

multiply_PiT_v(nu, mu, lut, v)[source]¶

Multiply the matrix $\mathbf{P_i}^{\mathrm{T}}$ by a vector $\underline{v}$ from the right. Do not construct the matrix explicitly.

Parameters:	nu – The list $\nu_i$ . mu – The list $\mu_i$ . lut – The lookup table. v – The vector $\underline{v} \in \mathbb{C}^{n(D,i)}$ .

multiply_Pi_v(nu, mu, lut, v)[source]¶

Multiply the matrix $\mathbf{P_i}$ by a vector $\underline{v}$ from the right. Do not construct the matrix explicitly.

Parameters:	nu – The list $\nu_i$ . mu – The list $\mu_i$ . lut – The lookup table. v – The vector $\underline{v} \in \mathcal{X}_i$ .

multiply_T_v(coeffs, K, NU, MU, D, J)[source]¶

Apply the transformation matrix $\mathbf{T}$ to the coefficients $\underline{c}$ .

Parameters:	coeffs – The coefficients vector $\underline{c}$ . K – The overlap matrix $\mathbf{K}$ . NU – The list of all $\nu_i$ . MU – The list of all $\mu_i$ . D – The dimension 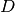$D$ . J – The maximal $l_1$ norm of any $\underline{k} \in \mathfrak{K}$ .

multiply_Tinv_v(coeffs, K, NU, MU, D, J)[source]¶

Apply the transformation matrix $\mathbf{T}^{-1}$ to the coefficients $\underline{d}$ .

Parameters:	coeffs – The coefficients vector $\underline{d}$ . K – The overlap matrix $\mathbf{K}$ . NU – The list of all $\nu_i$ . MU – The list of all $\mu_i$ . D – The dimension 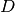$D$ . J – The maximal $l_1$ norm of any $\underline{k} \in \mathfrak{K}$ .

multiply_kronecker_power_v(D, A, v, i)[source]¶

Multiply the 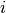$i$ -th Kronecker power of the matrix $\mathbf{A}$ by a vector $\underline{v}$ from the right.

Parameters:	D – The dimension 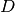$D$ . A – The matrix $\mathbf{A}$ . v – The vector $\underline{v}$ . i – The non-negative integer Kronecker power exponent.

Note

The matrix has to be square and of size $D^i$ .

overlap(D, Pi, eps)[source]¶

Compute the overlap matrix:

$\mathbf{K}_{r,c} := \langle \psi_{\underline{e_r}}[\Pi] | \phi_{\underline{e_c}}[\Pi] \rangle$

Parameters:	D – The dimension 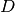$D$ . Pi – The parameter set $\Pi$ . eps – The semiclassical scaling parameter $\varepsilon$ .

transform_phi_to_psi(HAWPphi)[source]¶

Transform a old-kind wavepacket $\Phi[\Pi]$ into a new-kind wavepacket $\Psi[\Pi]$ .

Parameters:	HAWPphi – The wavepacket $\Phi[\Pi]$ to transform.
Returns:	A new wavepacket object representing $\Psi[\Pi]$ .

transform_psi_to_phi(HAWPpsi)[source]¶

Transform a new-kind wavepacket $\Psi[\Pi]$ into a old-kind wavepacket $\Phi[\Pi]$ .

Parameters:	HAWPpsi – The wavepacket $\Psi[\Pi]$ to transform.
Returns:	A new wavepacket object representing $\Phi[\Pi]$ .