InhomogeneousInnerProduct

About the InhomogeneousInnerProduct class

The WaveBlocks Project

@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License

Inheritance diagram

Inheritance diagram of InhomogeneousInnerProduct

Class documentation

class WaveBlocksND.InhomogeneousInnerProduct(delegate=None)[source]
__init__(delegate=None)[source]

This class computes the inhomogeneous inner product \langle\Psi|f|\Psi^\prime\rangle.

Parameters:delegate (A Quadrature subclass instance.) – The delegate inner product.
build_matrix(pacbra, packet=None, operator=None, eval_at_once=False)[source]

Delegates the computation of the matrix elements \langle\Psi|f|\Psi^\prime\rangle for a general function f(x) with x \in \mathbb{R}^D. The matrix is computed without including the coefficients c^i_k.

Parameters:
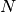  • pacbra – The wavepacket \Psi from the bra with N components.
  • packet – The wavepacket \Psi^\prime from the ket with N^\prime components.
  • operator – A matrix-valued function f(q, x): \mathbb{R} \times \mathbb{R}^D \rightarrow \mathbb{R}^{N \times N^\prime}.
  • eval_at_once (Boolean, default is False.) – Flag to tell whether the operator supports the entry=(r,c) call syntax.
Returns:

A matrix of size \sum_i^N |\mathfrak{K}_i| \times \sum_j^{N^\prime} |\mathfrak{K}^\prime_j|.
get_delegate()

Return the Quadrature subclass instance used for evaluation of this inner product.

Returns:The current instance of the quadrature.
get_description()[source]

Return a description of this inner product object. A description is a dict containing all key-value pairs necessary to reconstruct the current instance. A description never contains any data.

quadrature(pacbra, packet=None, operator=None, summed=False, component=None, diag_component=None, diagonal=False, eval_at_once=False)[source]

Delegates the evaluation of \langle\Psi|f|\Psi^\prime\rangle for a general function f(x) with x \in \mathbb{R}^D.

Parameters:
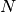  • pacbra – The wavepacket \Psi from the bra with N components.
  • packet – The wavepacket \Psi^\prime from the ket with N^\prime components.
  • operator – A matrix-valued function f(x): \mathbb{R}^D \rightarrow \mathbb{R}^{N \times N^\prime}.
  • summed (Boolean, default is False.) – Whether to sum up the individual integrals \langle\Phi_i|f_{i,j}|\Phi^\prime_j\rangle.
  • component – Request only the i-th component of the result. Remember that i \in [0, N \cdot N^\prime-1].
  • diag_component – Request only the i-th component from the diagonal entries, here i \in [0, N^\prime-1]. Note that component takes precedence over diag_component if both are supplied. (Which is discouraged)
  • diagonal – Only return the diagonal elements \langle\Phi_i|f_{i,i}|\Phi^\prime_i\rangle. This is useful for diagonal operators f.
  • eval_at_once (Boolean, default is False.) – Flag to tell whether the operator supports the entry=(r,c) call syntax.
Returns:

The value of the braket \langle\Psi|f|\Psi^\prime\rangle. This is either a scalar value or a list of N \cdot N^\prime scalar elements depending on the value of summed.
set_delegate(delegate)

Set the Quadrature subclass instance used for quadrature.

Parameters:delegate – The new Quadrature instance.