LimitedHyperbolicCutShape

About the LimitedHyperbolicCutShape class

The WaveBlocks Project

@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License

Inheritance diagram

Inheritance diagram of LimitedHyperbolicCutShape

Class documentation

class WaveBlocksND.LimitedHyperbolicCutShape(D, K, limits)[source]

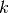This class implements the hyperbolic cut basis shape which is a special type of sparse basis set. A basis shape is essentially all information and operations related to the set \mathfrak{K} of multi-indices k. The hyperbolic cut shape in 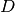D dimensions with sparsity 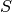S and limits K = (K_0,\ldots,K_{D-1}) is defined as the set

\mathfrak{K}(D, S, K) := \{ (k_0, \ldots, k_{D-1}) | 0 \leq k_d < K_d \forall d \in [0,\ldots,D-1] \land \prod_{d=0}^{D-1}(1+k_d) \leq S \}

__init__(D, K, limits)[source]
Parameters:
  • D – The dimension D
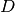
  • K – The sparsity parameter S
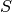
  • limits – The list of all limits \{K_d\}_{d=0}^{D-1}
__str__()[source]
Returns:A string describing the basis shape \mathfrak{K}.
__hash__()[source]

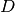Compute a unique hash for the basis shape. In the case of hyperbolic cut basis shapes \mathfrak{K} the basis is fully specified by its dimension D and the sparsity parameter K.

__getitem__(k)[source]

Make map look ups.

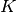__iter__()[source]

Implements iteration over the multi-indices 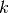k of the basis set \mathfrak{K}.

Note: The order of iteration is NOT fixed. If you need a special iteration scheme, use get_node_iterator().

__contains__(k)[source]

Checks if a given multi-index 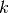k is part of the basis set \mathfrak{K}.

Parameters:k (tuple) – The multi-index 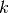k we want to test.
contains(k)[source]

Checks if a given multi-index 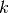k is part of the basis set \mathfrak{K}.

Parameters:k (tuple) – The multi-index 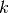k we want to test.
extend(tight=True)[source]

Extend the basis shape such that (at least) all neighbours of all boundary nodes are included in the extended basis shape.

Parameters:tight (Boolean, default is False) – Whether to cut off the long tails.
find_largest_index()

Find the index k \in \mathfrak{K} with maximal distance \sum_{d=0}^D k_d^2 from the zero index. In case of multiple maxima the method returns the first one found.

get_basis_size(extended=False)

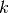Returns the size |\mathfrak{K}| of the basis. The size is the number of distinct multi-indices k that belong to the basis \mathfrak{K}.

Raise:NotImplementedError Abstract interface.
get_description()[source]

Return a description of this basis shape object. A description is a dict containing all key-value pairs necessary to reconstruct the current basis shape. A description never contains any data.

get_dimension()

Returns the dimension 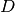D of the basis shape \mathfrak{K}. This is defined as the number of components each multi-index k = (k_0, \ldots, k_{D-1}) has.

Raise:NotImplementedError Abstract interface.
get_limits()[source]

Returns the upper limit K_d for all directions d.

Returns:A tuple of the maximum of the multi-index in each direction.
get_neighbours(k, selection=None, direction=None)[source]

Returns a list of all multi-indices that are neighbours of a given multi-index 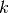k. A direct neighbour is defined as (k_0, \ldots, k_d \pm 1, \ldots, k_{D-1}) \forall d \in [0 \ldots D-1].

Parameters:
  • k (tuple) – The multi-index of which we want to get the neighbours.
  • selection (string with fixed values forward, backward or all. The values all is equivalent to the value None (default).) –
  • direction (int) – The direction 0 \leq d < D in which we want to find the neighbours k \pm e_d.
Returns:

A list containing the pairs (d, k^\prime).
get_node_iterator(mode='lex', direction=None)[source]

Returns an iterator to iterate over all basis elements k \in \mathfrak{K}.

Parameters:
  • mode (string) – The mode by which we iterate over the indices. Default is lex for lexicographical order. Supported is also chain, for the chain-like mode, details see the manual.
  • direction (integer.) – If iterating in chainmode this specifies the direction the chains go.