MatrixExponential¶
About the MatrixExponential functions¶
The WaveBlocks Project
@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License
Class documentation¶
The WaveBlocks Project
This file contains several different algorithms to compute the matrix exponential. Currently we have an exponential based on Pade approximations and an Arnoldi iteration method.
@author: R. Bourquin @copyright: Copyright (C) 2007 V. Gradinaru @copyright: Copyright (C) 2010, 2011, 2012, 2015 R. Bourquin @license: Modified BSD License
-
MatrixExponential.arnoldi(A, v0, k)[source]¶ Arnoldi algorithm to compute the Krylov approximation
 of a matrix
of a matrix  .
.Parameters: - A – The matrix
 of shape
of shape 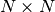 to approximate.
to approximate. - v0 – The initial vector
 of length
of length 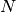 .
. - k – The number
 of Krylov steps performed.
of Krylov steps performed.
Returns: A tuple
 where
where  is the large matrix of shape
is the large matrix of shape
 containing the orthogonal vectors and
containing the orthogonal vectors and  is the
small matrix of shape
is the
small matrix of shape  containing the Krylov approximation
of
containing the Krylov approximation
of  .
.- A – The matrix
-
MatrixExponential.matrix_exp_arnoldi(A, v, factor, k)[source]¶ Compute the solution of
 via
via  steps of a the Arnoldi krylov method.
steps of a the Arnoldi krylov method.Parameters: - A – The matrix
 of shape
of shape 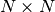 .
. - v – The vector
 of length
of length 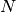 .
. - factor – An additional scalar factor
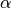 .
. - k – The number
 of Krylov steps performed.
of Krylov steps performed.
Returns: The (approximate) value of
 .
.- A – The matrix