MatrixPotential1S¶
About the MatrixPotential1S class¶
The WaveBlocks Project
@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License
Inheritance diagram¶

Class documentation¶
-
class
WaveBlocksND.MatrixPotential1S(expression, variables, **kwargs)[source]¶ This class represents a scalar potential
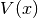 . The potential is
given as an analytic
. The potential is
given as an analytic  matrix expression. Some symbolic
calculations with the potential are supported.
matrix expression. Some symbolic
calculations with the potential are supported.-
calculate_eigenvalues()[source]¶ Calculate the eigenvalue
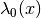 of the potential
of the potential 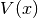 .
In the scalar case this is just equal to the matrix entry
.
In the scalar case this is just equal to the matrix entry 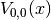 .
Note: This function is idempotent and the eigenvalues are memoized for later reuse.
.
Note: This function is idempotent and the eigenvalues are memoized for later reuse.
-
calculate_eigenvectors()[source]¶ Calculate the eigenvector
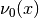 of the potential
of the potential 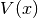 .
In the scalar case this is just the value
.
In the scalar case this is just the value 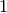 .
Note: This function is idempotent and the eigenvectors are memoized for later reuse.
.
Note: This function is idempotent and the eigenvectors are memoized for later reuse.
-
calculate_exponential(factor=1)[source]¶ Calculate the matrix exponential
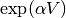 . In the
case of this class the matrix is of size
. In the
case of this class the matrix is of size 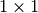 thus
the exponential simplifies to the scalar exponential function.
Note: This function is idempotent.
thus
the exponential simplifies to the scalar exponential function.
Note: This function is idempotent.Parameters: factor – The prefactor 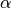 in the exponential.
in the exponential.
-
calculate_hessian()[source]¶ Calculate the Hessian matrix
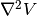 of the potential
of the potential 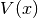 with
with 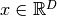 . For potentials which depend only one variable,
this equals the second derivative and
. For potentials which depend only one variable,
this equals the second derivative and 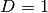 . Note that this function is idempotent.
. Note that this function is idempotent.
-
calculate_jacobian()[source]¶ Calculate the Jacobian matrix
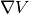 of the potential
of the potential 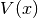 with
with 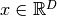 . For potentials which depend only one variable,
this equals the first derivative and
. For potentials which depend only one variable,
this equals the first derivative and 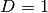 . Note that this function is idempotent.
. Note that this function is idempotent.
-
calculate_jacobian_canonical()[source]¶ Calculate the Jacobian matrix
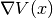 of the potential
of the potential 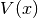 with
with 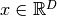 . For potentials which depend only one variable,
this equals the first derivative and
. For potentials which depend only one variable,
this equals the first derivative and 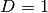 . Note that this function is idempotent.
. Note that this function is idempotent.
-
calculate_local_quadratic(diagonal_component=None)[source]¶ Calculate the local quadratic approximation
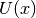 of the potential’s
eigenvalue
of the potential’s
eigenvalue 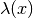 . Note that this function is idempotent.
. Note that this function is idempotent.Parameters: diagonal_component – Dummy parameter that has no effect here.
-
calculate_local_remainder(diagonal_component=None)[source]¶ Calculate the non-quadratic remainder
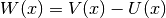 of the quadratic
Taylor approximation
of the quadratic
Taylor approximation 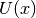 of the potential’s eigenvalue
of the potential’s eigenvalue 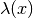 .
Note that this function is idempotent.
.
Note that this function is idempotent.Parameters: diagonal_component – Dummy parameter that has no effect here.
-
evaluate_at(grid, entry=None, as_matrix=False)[source]¶ Evaluate the potential
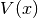 elementwise on a grid
elementwise on a grid  .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes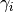 we want
to evaluate the potential at.
we want
to evaluate the potential at. - entry (A python tuple of two integers.) – The indices
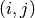 of the component
of the component 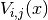 we want to evaluate or
we want to evaluate or Noneto evaluate all entries. This has no effect here as we only have a single entry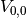 .
. - as_matrix – Dummy parameter which has no effect here.
Returns: A list containing a single numpy
ndarrayof shape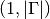 .
.- grid (A
-
evaluate_eigenvalues_at(grid, entry=None, as_matrix=False)[source]¶ Evaluate the eigenvalue
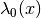 elementwise on a grid
elementwise on a grid 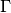 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes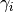 we want
to evaluate the eigenvalue at.
we want
to evaluate the eigenvalue at. - entry (A python tuple of two integers.) – The indices
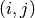 of the component
of the component 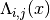 we want to evaluate or
we want to evaluate or Noneto evaluate all entries. If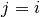 then we evaluate the eigenvalue
then we evaluate the eigenvalue 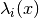 . This has no
effect here as we only have a single entry
. This has no
effect here as we only have a single entry 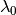 .
. - as_matrix – Dummy parameter which has no effect here.
Returns: A list containing a single numpy ndarray of shape
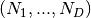 .
.- grid (A
-
evaluate_eigenvectors_at(grid, entry=None)[source]¶ Evaluate the eigenvector
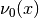 elementwise on a grid
elementwise on a grid 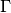 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes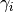 we want
to evaluate the eigenvector at.
we want
to evaluate the eigenvector at. - entry (A singly python integer.) – The index
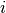 of the eigenvector
of the eigenvector 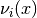 we want to evaluate or
we want to evaluate or Noneto evaluate all eigenvectors. This has no effect here as we only have a single entry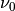 .
.
Returns: A list containing the numpy ndarrays, all of shape
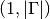 .
.- grid (A
-
evaluate_exponential_at(grid, entry=None)[source]¶ Evaluate the exponential of the potential matrix
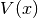 on a grid
on a grid 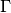 .
.Parameters: grid (A Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes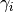 we want
to evaluate the exponential at.
we want
to evaluate the exponential at.Returns: The numerical approximation of the matrix exponential at the given grid nodes.
-
evaluate_hessian_at(grid, component=None)[source]¶ Evaluate the potential’s Hessian
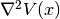 at some grid
nodes
at some grid
nodes 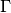 .
.Parameters: - grid – The grid nodes
 the Hessian gets evaluated at.
the Hessian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s Hessian at the given nodes. The result is an
ndarrayof shape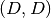 is we evaluate at a single
grid node or of shape
is we evaluate at a single
grid node or of shape 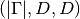 if we evaluate at multiple
nodes simultaneously.
if we evaluate at multiple
nodes simultaneously.- grid – The grid nodes
-
evaluate_jacobian_at(grid, component=None)[source]¶ Evaluate the potential’s Jacobian
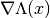 at some grid
nodes
at some grid
nodes 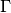 .
.Parameters: - grid – The grid nodes
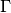 the Jacobian gets evaluated at.
the Jacobian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s Jacobian at the given nodes. The result is an
ndarrayof shape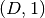 is we evaluate at a single
grid node or of shape
is we evaluate at a single
grid node or of shape 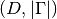 if we evaluate at multiple nodes simultaneously.
if we evaluate at multiple nodes simultaneously.- grid – The grid nodes
-
evaluate_jacobian_canonical_at(grid, component=None)[source]¶ Evaluate the potential’s Jacobian
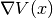 at some grid
nodes
at some grid
nodes 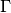 .
.Parameters: - grid – The grid nodes
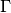 the Jacobian gets evaluated at.
the Jacobian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s Jacobian at the given nodes. The result is an
ndarrayof shape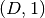 is we evaluate at a single
grid node or of shape
is we evaluate at a single
grid node or of shape 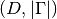 if we evaluate at multiple nodes simultaneously.
if we evaluate at multiple nodes simultaneously.- grid – The grid nodes
-
evaluate_local_quadratic_at(grid, diagonal_component=None)[source]¶ Numerically evaluate the local quadratic approximation
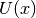 of
the potential’s eigenvalue
of
the potential’s eigenvalue 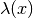 at the given grid nodes
at the given grid nodes 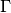 .
This function is used for the homogeneous case.
.
This function is used for the homogeneous case.Parameters: - grid – The grid nodes
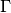 the quadratic approximation gets evaluated at.
the quadratic approximation gets evaluated at. - diagonal_component – Dummy parameter that has no effect here.
Returns: A list containing the values
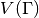 ,
, 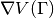 and
and
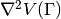 .
.- grid – The grid nodes
-
evaluate_local_remainder_at(grid, position, diagonal_component=None, entry=None)[source]¶ Numerically evaluate the non-quadratic remainder
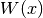 of the quadratic
approximation
of the quadratic
approximation 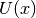 of the potential’s eigenvalue
of the potential’s eigenvalue 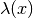 at the
given nodes
at the
given nodes 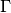 .
.Parameters: - grid – The grid nodes
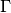 the remainder
the remainder 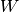 gets evaluated at.
gets evaluated at. - position – The point
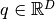 where the Taylor series is computed.
where the Taylor series is computed. - diagonal_component – Dummy parameter that has no effect here.
- entry – Dummy parameter that has no effect here.
Returns: A list with a single entry consisting of an
ndarraycontaining the values of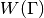 . The array is of shape
. The array is of shape 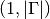 .
.- grid – The grid nodes
-
get_dimension()¶ Return the dimension
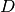 of the potential
of the potential 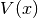 .
The dimension is equal to the number of free variables
.
The dimension is equal to the number of free variables 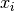 where
where 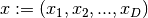 .
.
-
get_number_components()¶ Return the number
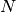 of components the potential
of components the potential 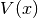 supports. This is equivalent to the number of energy levels
supports. This is equivalent to the number of energy levels 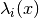 .
.
-