Propagator¶

About the `Propagator` class¶

The WaveBlocks Project

Inheritance diagram¶

Class documentation¶

class WaveBlocksND.Propagator[source]¶

Propagators can numerically simulate the time evolution of quantum states $\psi(x,t)$ as described by the time-dependent Schroedinger equation

$i \varepsilon^2 \frac{\partial}{\partial t} \psi(x,t) = H \psi(x,t)$

where the semi-classical scaling parameter $\varepsilon > 0$ is already included. The Hamiltonian operator $H$ is defined as

$H = T + V(x) = -\frac{\varepsilon^4}{2} \Delta + V(x)$

get_number_components()[source]¶

Returns:	The number 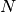$N$ components of $\psi(x,t)$ .
Raise:	`NotImplementedError` This is an abstract base class.

get_potential()[source]¶

Returns the potential 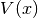$V(x)$ used for time propagation.

Returns:	A `MatrixPotential` subclass instance.

post_propagate()[source]¶

Given the wavefunction $\psi$ at final time $T$ , perform some computations exactly once after running the ordinary time propagation and before each time simulation data will be saved.

This method does not raise an exception but instead just does nothing and returns.

pre_propagate()[source]¶

Given the wavefunction $\psi$ at initial time $t_0$ , perform some computations exactly once before running the ordinary time propagation and after each time simulation data was saved.