SemiclassicalPropagator¶
About the SemiclassicalPropagator class¶
The WaveBlocks Project
@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License
Inheritance diagram¶

Class documentation¶
-
class
WaveBlocksND.SemiclassicalPropagator(parameters, potential, packets=[])[source]¶ This class can numerically propagate given initial values
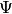 in
a potential
in
a potential 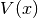 . The propagation is done for a given set of homogeneous
Hagedorn wavepackets neglecting interaction.
. The propagation is done for a given set of homogeneous
Hagedorn wavepackets neglecting interaction.-
__init__(parameters, potential, packets=[])[source]¶ Initialize a new
SemiclassicalPropagatorinstance.Parameters: - parameters (A
ParameterProviderinstance) – AParameterProviderinstance containing at least the keydtfor providing the timestep .
. - potential – The potential
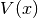 the wavepacket
the wavepacket 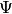 feels during the time propagation.
feels during the time propagation. - packet – The initial homogeneous Hagedorn wavepacket
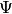 we propagate in time.
we propagate in time.
Raises: ValueError – If the number of components of
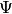 does not match
the number of energy levels
does not match
the number of energy levels 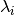 of the potential.
of the potential.- parameters (A
-
add_wavepacket(packet)[source]¶ Add a new wavepacket
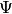 to the list of propagated wavepackets.
to the list of propagated wavepackets.Parameters: packet (A tuple  with
with 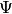 a
a HagedornWavepacketinstance and an integer.) – The new wavepacket
an integer.) – The new wavepacket 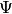 and its leading component
and its leading component ![\chi \in [0,N-1]](../_images/math/b07aef8fb164e62cacfd4be92bc7aa04b49d6f7b.png) .
.
-
build(method)¶ Parameters: method – A string specifying the method for time integration. Returns: Two arrays  and
and  .
.Method Order Authors Reference LT 1 Lie/Trotter [1], [3] page 42, equation 5.2 S2 2 Strang [2], [3] page 42, equation 5.3 SS 2 Strang [2], [3] page 42, equation 5.3 PRKS6 4 Blanes/Moan [4] page 318, table 2, ‘S6’ BM42 4 Blanes/Moan [4] page 318, table 3, ‘SRKNb6’ Y4 4 Yoshida [5], [3] page 40, equation 4.4 Y61 6 Yoshida [5], [3] page 144, equation 3.11 BM63 6 Blanes/Moan [4] page 318, table 3, ‘SRKNa14’ KL6 6 Kahan/Li [6], [3] page 144, equation 3.12 KL8 8 Kahan/Li [6], [3] page 145, equation 3.14 KL10 10 Kahan/Li [6], [3] page 146, equation 3.15 [1] H.F. Trotter, “On the product of semi-groups of operators”, Proc. Am. Math. Soc.1O (1959) 545-551. [2] (1, 2) G. Strang, “On the construction and comparison of difference schemes”, SIAM J. Numer. Anal. 5 (1968) 506-517. [3] (1, 2, 3, 4, 5, 6, 7, 8) E. Hairer, C. Lubich, and G. Wanner, “Geometric Numerical Integration - Structure-Preserving Algorithms for Ordinary Differential Equations”, Springer-Verlag, New York, 2002 (Corrected second printing 2004). [4] (1, 2, 3) S. Blanes and P.C. Moan, “Practical Symplectic Partitioned Runge-Kutta and Runge-Kutta-Nystrom Methods”, J. Computational and Applied Mathematics, Volume 142, Issue 2, (2002) 313-330. [5] (1, 2) H. Yoshida, “Construction of higher order symplectic integrators”, Phys. Lett. A 150 (1990) 262-268. [6] (1, 2, 3) W. Kahan and R.-c. Li, “Composition constants for raising the orders of unconventional schemes for ordinary differential equations”, Math. Comput. 66 (1997) 1089-1099.
-
get_potential()¶ Returns the potential
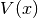 used for time propagation.
used for time propagation.Returns: A MatrixPotentialsubclass instance.
-
get_wavepackets(packet=None)[source]¶ Return the wavepackets
 that take part in the time propagation by the
current
that take part in the time propagation by the
current SemiclassicalPropagatorinstance.Parameters: packet (Integer or None) – The index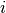 (in this list) of a single packet
(in this list) of a single packet  that is
to be returned. If set to
that is
to be returned. If set to None(default) return the full list with all packets.Returns: A list of HagedornWavepacketinstances or a single instance.
-
intsplit(psi1, psi2, a, b, tspan, N, args1=[], args2=[])¶ Compute a single, full propagation step by operator splitting.
Parameters: - psi1 – First evolution operator

- psi2 – Second evolution operator

- a – Parameters for evolution with

- b – Parameters for evolution with

- tspan – Timespan
 of a single, full splitting step
of a single, full splitting step - N – Number of substeps to perform
- args1 – Additional optional arguments of

- args2 – Additional optional arguments of

Note
The values for
args1andargs2have to be of typelisteven in case of single items.- psi1 – First evolution operator
-
order(method)¶ Parameters: method – A string specifying the method for time integration. Returns: The order of this method.
-
post_propagate()¶ Given the wavefunction
 at final time
at final time  ,
perform some computations exactly once after running the ordinary
time propagation and before each time simulation data will be saved.
,
perform some computations exactly once after running the ordinary
time propagation and before each time simulation data will be saved.This method does not raise an exception but instead just does nothing and returns.
-
pre_propagate()¶ Given the wavefunction
 at initial time
at initial time  ,
perform some computations exactly once before running the ordinary
time propagation and after each time simulation data was saved.
,
perform some computations exactly once before running the ordinary
time propagation and after each time simulation data was saved.This method does not raise an exception but instead just does nothing and returns.
-
propagate()[source]¶ Given a wavepacket
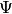 at time
at time  compute the propagated
wavepacket at time
compute the propagated
wavepacket at time  . We perform exactly one timestep of size
. We perform exactly one timestep of size
 here. This propagation is done for all packets in the list
here. This propagation is done for all packets in the list
 and neglects any interaction between two packets.
The semiclassical propagation scheme is used.
and neglects any interaction between two packets.
The semiclassical propagation scheme is used.More details can be found in [7].
[7] V. Gradinaru and G.A. Hagedorn, “Convergence of a semiclassical wavepacket based time-splitting for the Schroedinger equation”, Numerische Mathematik, volume 126 number 1 (2013) 53-73.
-
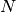 of components
of components 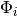 of
of  tuples.) – A list of new wavepackets
tuples.) – A list of new wavepackets  to propagate.
to propagate.