SmolyakQR

About the SmolyakQR class

The WaveBlocks Project

@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License

Inheritance diagram

Inheritance diagram of SmolyakQR

Class documentation

class WaveBlocksND.SmolyakQR(dimension, level, rules, options={})[source]

This class implements the construction of high dimensional quadrature rules from one-dimensional ones by applying the Smolyak construction.

__init__(dimension, level, rules, options={})[source]

Initialize a SmolyakQR instance.

Parameters:
  • dimension – The dimension 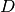D of the final quadrature rule.
  • level – The level k of the Smolyak construction. From theory we know that a Smolyak rule of order k is exact up to 2 k - 1 if the individual rules Q_i are exact up to 2 i - 1. The level has to be larger than or equal 1.
  • rules – A collection of QuadratureRule subclass instances. Their nodes and weights will be used in the Smolyak construction.

Note

The rules object must implement simple indexing by non-negative numbers and for a given index j return a univariate quadrature rule of order j. Special attention must be payed in case this object is mutable. We do not copy it.

Warning

This implementation uses a special optimization that speeds up the computation of all quadrature nodes, especially in high dimension, but is only valid if all one dimensional rules have symmetric nodes and weights. That is, for every node weight pair (\gamma, \omega) that is part of the rule, the pair (-\gamma, \omega) is also contained in the quadrature rule.

construct_rule(K, tolerance=1e-15)[source]

Compute the quadrature nodes \{\gamma_i\}_i and quadrature weights \{\omega_i\}_i.

Parameters:
  • K – The level K of the Smolyak construction.
  • tolerance – Tolerance for dropping identical quadrature nodes.

Note

This is an internal method and there should be no reason to explicitely call it manually.

Warning

This method is very expensive and may take a long time to finish. Also, the quadrature nodes may use large amounts of memory depending on the dimension and level parameters.

get_description()[source]

Return a description of this quadrature rule object. A description is a dict containing all key-value pairs necessary to reconstruct the current instance. A description never contains any data.

get_dimension()
Returns:The space dimension 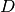D of the quadrature rule.
get_nodes(flat=True, split=False)[source]

Returns the quadrature nodes \{\gamma_i\}_i.

Parameters:
  • flat (Boolean, default is True.) – Dummy parameter for API compatibility with Grids.
  • split (Boolean, default is False.) – Dummy parameter for API compatibility with Grids.
Returns:

An ndarray containing the quadrature nodes \{\gamma_i\}_i.
get_number_nodes()
Returns:The number of quadrature nodes denoted by |\Gamma| that are part of this quadrature rule \Gamma = (\gamma, \omega).
get_weights()[source]

Returns the quadrature weights \{\omega_i\}_i.

Returns:An ndarray containing the quadrature weights \{\omega_i\}_i.