MatrixPotential2S¶
About the MatrixPotential2S class¶
The WaveBlocks Project
@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License
Inheritance diagram¶

Class documentation¶
-
class
WaveBlocksND.MatrixPotential2S(expression, variables, **kwargs)[source]¶ This class represents a matrix potential
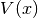 . The potential is
given as an analytic
. The potential is
given as an analytic 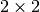 matrix expression. Some symbolic
calculations with the potential are supported.
matrix expression. Some symbolic
calculations with the potential are supported.-
calculate_eigenvalues()[source]¶ Calculate the two eigenvalues
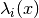 of the potential
of the potential 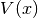 .
We can do this by symbolic calculations. The multiplicities are taken into account.
Note: This function is idempotent and the eigenvalues are memoized for later reuse.
.
We can do this by symbolic calculations. The multiplicities are taken into account.
Note: This function is idempotent and the eigenvalues are memoized for later reuse.
-
calculate_eigenvectors()[source]¶ Calculate the two eigenvectors
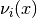 of the potential
of the potential 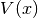 .
We can do this by symbolic calculations.
Note: This function is idempotent and the eigenvectors are memoized for later reuse.
.
We can do this by symbolic calculations.
Note: This function is idempotent and the eigenvectors are memoized for later reuse.
-
calculate_exponential(factor=1)[source]¶ Calculate the matrix exponential
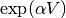 . In the case
of this class the matrix is of size
. In the case
of this class the matrix is of size 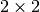 thus the exponential
can be calculated analytically for a general matrix.
Note: This function is idempotent.
thus the exponential
can be calculated analytically for a general matrix.
Note: This function is idempotent.Parameters: factor – The prefactor 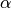 in the exponential.
in the exponential.
-
calculate_hessian()[source]¶ Calculate the Hessian matrix
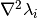 of the potential’s
eigenvalues
of the potential’s
eigenvalues 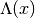 with
with 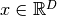 . For potentials
which depend only one variable, this equals the second derivative and
. For potentials
which depend only one variable, this equals the second derivative and 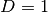 .
Note that this function is idempotent.
.
Note that this function is idempotent.
-
calculate_jacobian()[source]¶ Calculate the Jacobian matrix
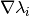 of the potential’s
eigenvalues
of the potential’s
eigenvalues 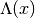 with
with 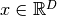 . For potentials
which depend only one variable, this equals the first derivative and
. For potentials
which depend only one variable, this equals the first derivative and 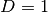 .
Note that this function is idempotent.
.
Note that this function is idempotent.
-
calculate_local_quadratic(diagonal_component=None)[source]¶ Calculate the local quadratic approximation matrix
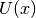 of the potential’s
eigenvalues in
of the potential’s
eigenvalues in 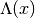 . This function can be used for the homogeneous case
and takes into account the leading component
. This function can be used for the homogeneous case
and takes into account the leading component ![\chi \in [0,\ldots,N-1]](../_images/math/f71172924ecfe7f4d848e2c7b91533bdacd6e3e3.png) .
If the parameter
.
If the parameter 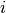 is not given, calculate the local quadratic approximation
matrix
is not given, calculate the local quadratic approximation
matrix 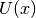 of all the potential’s eigenvalues in
of all the potential’s eigenvalues in  . This case
can be used for the inhomogeneous case.
. This case
can be used for the inhomogeneous case.Parameters: diagonal_component (Integer or None(default)) – Specifies the index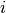 of the eigenvalue
of the eigenvalue 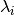 that gets expanded into a Taylor series
that gets expanded into a Taylor series 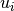 .
.
-
calculate_local_remainder(diagonal_component=None)[source]¶ Calculate the non-quadratic remainder matrix
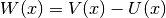 of the
quadratic approximation matrix
of the
quadratic approximation matrix 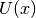 of the potential’s eigenvalue matrix
of the potential’s eigenvalue matrix
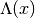 . In the homogeneous case the matrix
. In the homogeneous case the matrix 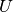 is given by
is given by
![U(x) = \text{diag}([u_i,\ldots,u_i])](../_images/math/2dc5f0b223e940d29f837a22916cb3a5706f823e.png) where in the inhomogeneous case it
is given by
where in the inhomogeneous case it
is given by ![U(x) = \text{diag}([u_0,\ldots,u_{N-1}])](../_images/math/cf179063d19268efeea161090a20161a9f3cd32d.png) .
.Parameters: diagonal_component (Integer or None(default)) – Specifies the index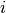 of the eigenvalue
of the eigenvalue 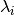 that gets expanded into a Taylor series
that gets expanded into a Taylor series 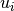 . If set to
. If set to
Nonethe inhomogeneous case is computed.
-
evaluate_at(grid, entry=None, as_matrix=True)[source]¶ Evaluate the potential
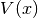 elementwise on a grid
elementwise on a grid 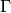 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes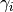 we want
to evaluate the potential at.
we want
to evaluate the potential at. - entry (A python tuple of two integers.) – The indices
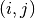 of the component
of the component 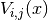 we want to evaluate or
we want to evaluate or Noneto evaluate all entries. - as_matrix – Dummy parameter which has no effect here.
Returns: A list containing 4 numpy ndarrays of shape
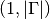 .
.- grid (A
-
evaluate_eigenvalues_at(grid, entry=None, as_matrix=False)[source]¶ Evaluate the eigenvalues
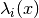 elementwise on a grid
elementwise on a grid 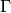 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid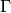 containing the nodes
containing the nodes 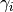 we want
to evaluate the eigenvalues at.
we want
to evaluate the eigenvalues at. - entry (A python tuple of two integers.) – The indices
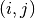 of the component
of the component 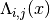 we want to evaluate or
we want to evaluate or Noneto evaluate all entries. If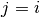 then we evaluate the eigenvalue
then we evaluate the eigenvalue 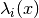 .
. - as_matrix – Whether to include the off-diagonal zero entries of
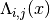 in the return value.
in the return value.
Returns: A list containing the numpy
ndarray, all of shape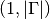 .
.- grid (A
-
evaluate_eigenvectors_at(grid, entry=None)[source]¶ Evaluate the two eigenvectors
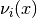 elementwise on a grid
elementwise on a grid 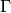 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes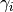 we want
to evaluate the eigenvectors at.
we want
to evaluate the eigenvectors at. - entry (A single python integer.) – The index
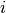 of the eigenvector
of the eigenvector 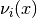 we want to evaluate or
we want to evaluate or Noneto evaluate all eigenvectors.
Returns: A list containing the numpy ndarrays, all of shape
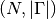 .
.- grid (A
-
evaluate_exponential_at(grid)[source]¶ Evaluate the exponential of the potential matrix
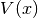 on a grid
on a grid 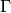 .
.Parameters: grid (A Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes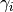 we want
to evaluate the exponential at.
we want
to evaluate the exponential at.Returns: The numerical approximation of the matrix exponential at the given grid nodes. A list contains the exponentials for all entries 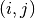 , each having the
same shape as the grid.
, each having the
same shape as the grid.
-
evaluate_hessian_at(grid, component=None)[source]¶ Evaluate the list of Hessian matrices
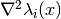 at some grid
nodes
at some grid
nodes  .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid nodes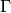 the Hessian gets evaluated at.
the Hessian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s Hessian at the given nodes. The result is an
ndarrayof shape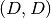 is we evaluate at a single
grid node or of shape
is we evaluate at a single
grid node or of shape 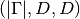 if we evaluate at multiple
nodes simultaneously.
if we evaluate at multiple
nodes simultaneously.- grid (A
-
evaluate_jacobian_at(grid, component=None)[source]¶ Evaluate the list of Jacobian matrices
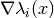 at some grid
nodes
at some grid
nodes 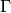 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid nodes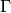 the Jacobian gets evaluated at.
the Jacobian gets evaluated at. - component – Dummy parameter that has no effect here.
Returns: The value of the potential’s Jacobian at the given nodes. The result is a list of
ndarrayeach of shape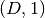 is we evaluate
at a single grid node or of shape
is we evaluate
at a single grid node or of shape 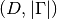 if we evaluate at multiple nodes simultaneously.
if we evaluate at multiple nodes simultaneously.- grid (A
-
evaluate_local_quadratic_at(grid, diagonal_component=None)[source]¶ Numerically evaluate the local quadratic approximation matrix
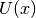 of
the potential’s eigenvalues in
of
the potential’s eigenvalues in 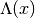 at the given grid nodes
at the given grid nodes 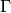 .
.Parameters: - grid (A
Gridinstance. (Numpy arrays are not directly supported yet.)) – The grid containing the nodes
containing the nodes 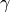 we want to
evaluate the quadratic approximation at.
we want to
evaluate the quadratic approximation at. - diagonal_component – Specifies the index
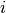 of the eigenvalue
of the eigenvalue 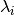 that gets expanded into a Taylor series
that gets expanded into a Taylor series 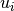 .
.
Returns: A list of tuples or a single tuple. Each tuple
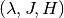 contains the
the evaluated eigenvalues
contains the
the evaluated eigenvalues 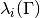 , the Jacobian
, the Jacobian 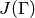 and the Hessian
and the Hessian 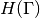 in this order.
in this order.- grid (A
-
evaluate_local_remainder_at(grid, position, diagonal_component=None, entry=None)[source]¶ Numerically evaluate the non-quadratic remainder
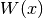 of the quadratic
approximation
of the quadratic
approximation 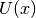 of the potential’s eigenvalue
of the potential’s eigenvalue 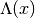 at the
given nodes
at the
given nodes 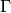 .Warning: do not set the
.Warning: do not set thediagonal_componentand theentryparameter both toNone.Parameters: - grid – The grid nodes
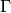 the remainder
the remainder 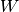 gets evaluated at.
gets evaluated at. - position – The point
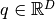 where the Taylor series is computed.
where the Taylor series is computed. - diagonal_component (Integer or
None(default)) – Specifies the index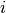 of the eigenvalue
of the eigenvalue 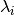 that gets expanded into a Taylor series
that gets expanded into a Taylor series 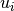 and whose
remainder matrix
and whose
remainder matrix ![W(x) = V(x) - \text{diag}([u_i,\ldots,u_i])](../_images/math/b03b7cf72e5b53dbaba8fbcec763c9f8f46a1434.png) we evaluate. If set to
we evaluate. If set to Nonethe inhomogeneous case given by![W(x) = V(x) - \text{diag}([u_0,\ldots,u_{N-1}])](../_images/math/57b61314cefee8e2e4d21d95a07a156dc5530c51.png) is computed.
is computed. - entry (A python tuple of two integers.) – The entry
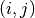 of the remainder matrix
of the remainder matrix 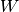 that is evaluated.
that is evaluated.
Returns: A list with
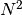
ndarrayelements or a singlendarray. Each containing the values of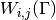 . Each array is of shape
. Each array is of shape
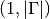 .
.- grid – The grid nodes
-
get_dimension()¶ Return the dimension
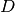 of the potential
of the potential 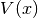 .
The dimension is equal to the number of free variables
.
The dimension is equal to the number of free variables 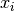 where
where 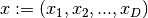 .
.
-
get_number_components()¶ Return the number
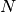 of components the potential
of components the potential 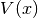 supports. This is equivalent to the number of energy levels
supports. This is equivalent to the number of energy levels 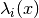 .
.
-