Pre764scPropagator

About the Pre764scPropagator class

The WaveBlocks Project

@author: R. Bourquin @copyright: Copyright (C) 2010, 2011, 2012, 2013, 2014, 2015, 2016 R. Bourquin @license: Modified BSD License

Inheritance diagram

Inheritance diagram of Pre764scPropagator

Class documentation

class WaveBlocksND.Pre764scPropagator(parameters, potential, packets=[])[source]

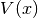This class can numerically propagate given initial values \Psi in a potential V(x). The propagation is done for a given set of homogeneous Hagedorn wavepackets neglecting interaction. It uses the preprocessor 764 method, see Blanes, Casas, Ros 2000, table IV and the idea of the semiclassical splitting

__init__(parameters, potential, packets=[])[source]

Initialize a new SemiclassicalPropagator instance.

Parameters:
  • parameters (A ParameterProvider instance) – A ParameterProvider instance containing at least the key dt for providing the timestep \tau.
  • potential – The potential 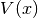V(x) the wavepacket \Psi feels during the time propagation.
  • packet – The initial homogeneous Hagedorn wavepacket \Psi we propagate in time.
Raises:

ValueError – If the number of components of \Psi does not match the number of energy levels \lambda_i of the potential.
add_wavepacket(packet)[source]

Add a new wavepacket \Psi to the list of propagated wavepackets.

Parameters:packet (A tuple (\Psi, \chi) with \Psi a HagedornWavepacket instance and \chi an integer.) – The new wavepacket \Psi and its leading component \chi \in [0,N-1].
build(method)
Parameters:method – A string specifying the method for time integration.
Returns:Two arrays a and b.
Method Order Authors Reference
LT 1 Lie/Trotter [1], [3] page 42, equation 5.2
S2 2 Strang [2], [3] page 42, equation 5.3
SS 2 Strang [2], [3] page 42, equation 5.3
PRKS6 4 Blanes/Moan [4] page 318, table 2, ‘S6’
BM42 4 Blanes/Moan [4] page 318, table 3, ‘SRKNb6’
Y4 4 Yoshida [5], [3] page 40, equation 4.4
Y61 6 Yoshida [5], [3] page 144, equation 3.11
BM63 6 Blanes/Moan [4] page 318, table 3, ‘SRKNa14’
KL6 6 Kahan/Li [6], [3] page 144, equation 3.12
KL8 8 Kahan/Li [6], [3] page 145, equation 3.14
KL10 10 Kahan/Li [6], [3] page 146, equation 3.15
[1]H.F. Trotter, “On the product of semi-groups of operators”, Proc. Am. Math. Soc.1O (1959) 545-551.
[2](1, 2) G. Strang, “On the construction and comparison of difference schemes”, SIAM J. Numer. Anal. 5 (1968) 506-517.
[3](1, 2, 3, 4, 5, 6, 7, 8) E. Hairer, C. Lubich, and G. Wanner, “Geometric Numerical Integration - Structure-Preserving Algorithms for Ordinary Differential Equations”, Springer-Verlag, New York, 2002 (Corrected second printing 2004).
[4](1, 2, 3) S. Blanes and P.C. Moan, “Practical Symplectic Partitioned Runge-Kutta and Runge-Kutta-Nystrom Methods”, J. Computational and Applied Mathematics, Volume 142, Issue 2, (2002) 313-330.
[5](1, 2) H. Yoshida, “Construction of higher order symplectic integrators”, Phys. Lett. A 150 (1990) 262-268.
[6](1, 2, 3) W. Kahan and R.-c. Li, “Composition constants for raising the orders of unconventional schemes for ordinary differential equations”, Math. Comput. 66 (1997) 1089-1099.
get_number_components()[source]
Returns:The number N of components \Phi_i of \Psi.
get_potential()

Returns the potential 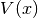V(x) used for time propagation.

Returns:A MatrixPotential subclass instance.
get_wavepackets(packet=None)[source]

Return the wavepackets \{\Psi_i\}_i that take part in the time propagation by the current SemiclassicalPropagator instance.

Parameters:packet (Integer or None) – The index i (in this list) of a single packet \Psi_i that is to be returned. If set to None (default) return the full list with all packets.
Returns:A list of HagedornWavepacket instances or a single instance.
intsplit(psi1, psi2, a, b, tspan, N, args1=[], args2=[])

Compute a single, full propagation step by operator splitting.

Parameters:
  • psi1 – First evolution operator \Psi_a
  • psi2 – Second evolution operator \Psi_b
  • a – Parameters for evolution with \Psi_a
  • b – Parameters for evolution with \Psi_b
  • tspan – Timespan t of a single, full splitting step
  • N – Number of substeps to perform
  • args1 – Additional optional arguments of \Psi_a
  • args2 – Additional optional arguments of \Psi_b

Note

The values for args1 and args2 have to be of type list even in case of single items.

order(method)
Parameters:method – A string specifying the method for time integration.
Returns:The order of this method.
post_propagate()[source]

Given the wavefunction \psi at final time T, perform some computations exactly once after running the ordinary time propagation.

pre_propagate()[source]

Given the wavefunction \psi at initial time t_0, perform some computations exactly once before running the ordinary time propagation.

propagate()[source]

Given a wavepacket \Psi at time t compute the propagated wavepacket at time t + \tau. We perform exactly one timestep of size \tau here. This propagation is done for all packets in the list \{\Psi_i\}_i and neglects any interaction between two packets.

More details can be found in [7].

[7]
  1. Blanes, R. Bourquin and V. Gradinaru, “Raising the Order of Convergence in the Semiclassical Splitting”.
set_wavepackets(packetlist)[source]

Set the list \{\Psi_i\}_i of wavepackets that the propagator will propagate.

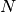Parameters:packetlist (A list of (\Psi_i, \chi_i) tuples.) – A list of new wavepackets \Psi_i and their leading components \chi_i to propagate.